Selected Publication List
Junyi Yang, Hidemaro Suwa*, Derek Meyers, Han Zhang, Lukas Horak, Zhan Zhang, Evguenia Karapetrova, Jong-Woo Kim, Philip J. Ryan, Mark P. M. Dean, Lin Hao*, and Jian Liu∗, Nano Lett. 23, 11409 (2023).
Extraordinary Magnetic Response of an Anisotropic 2D Antiferromagnet via Site Dilution
Hidemaro Suwa, Justin S. Smith, Nicholas Lubbers, Cristian D. Batista, Gia-Wei Chern, and Kipton Barros, Phys. Rev. B 99, 161107(R) (2019).
Machine learning for molecular dynamics with strongly correlated electrons
Hidemaro Suwa, Arnab Sen, and Anders W. Sandvik, Phys. Rev. B 94, 144416 (2016).
Hidemaro Suwa and Synge Todo, Phys. Rev. Lett. 115, 080601 (2015).
Generalized Moment Method for Gap Estimation and Quantum Monte Carlo Level Spectroscopy
Hidemaro Suwa, Springer Theses (2014).
Geometrically Constructed Markov Chain Monte Carlo Study of Quantum Spin-phonon Complex Systems
Hidemaro Suwa and Synge Todo, Phys. Rev. Lett. 105, 120603 (2010).
Developments of Markov chain Monte Carlo methods
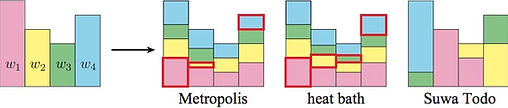
Markov chain Monte Carlo (MCMC) method is a vital numerical tool for systems with many degrees of freedom, particularly for strongly correlated systems. Since it was invented by Metropolis et al. in 1953, the MCMC method has evolved under detailed balance, which is, however, not necessary. We invented an algorithm for Monte Carlo sampling without detailed balance, using the geometric allocation of probability. Our algorithm outperforms the Metropolis algorithm and the Gibbs sampler in many cases. This approach is generally applicable to many kinds of MCMC methods.
References
Hidemaro Suwa and Synge Todo, Phys. Rev. Lett. 105, 120603 (2010).
Markov Chain Monte Carlo Method without Detailed Balance
Synge Todo and Hidemaro Suwa, J. Phys.:Conf. Ser., 473, 012013 (2013).
Geometric Allocation Approaches in Markov Chain Monte Carlo
Hidemaro Suwa, Physica A: Statistical Mechanics and its Applications 633, 129368 (2024).
Reducing rejection exponentially improves Markov chain Monte Carlo sampling
Fig. Example of geometric allocation of probability in the cases of the Metropolis, the heat bath (Gibbs sampler), and the Suwa-Todo algorithms.
Dynamical Simulations
Dynamical structure factor is an important quantity for studying excitation and dynamics of physical systems. Although extensively measured experimentally (e.g. by inelastic neutron scattering), it is not easy to calculate accurately in a theoretical approach. We developed an efficient method for dynamics of spin-density waves and calculated the dynamical spin structure factor for large systems of the Hubbard model.
References
Gia-Wei Chern, Kipton Barros, Zhentao Wang, Hidemaro Suwa, and Cristian D Batista, Phys. Rev. B 97, 035120 (2018).
Semiclassical dynamics of spin density waves
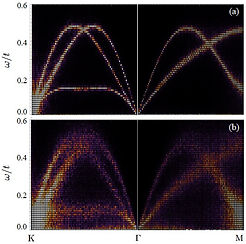
Fig. Dynamical spin structure factor for the 120 deg. order of the (a) Hubbard and (b) Anderson-Hubbard models. The number of sites is 120×120. The figure is taken from G. Chern et al., (2017).
Deconfined quantum criticality
Many phase transitions are described by the Landau-Ginzburg-Wilson (LGW) paradigm where an effective action is expanded in powers of an order parameter and its derivatives. Recently, the deconfined quantum criticality has caught a great deal of attention as a highly non-trivial phase-transition point beyond the LGW paradigm. The low energy physics is described not by the original degrees of freedom manifest in the model Hamiltonian but by internal degrees of freedom emerging as fractional excitation. We studied the excitation energy around the deconfined quantum-critical point in the two-dimensional quantum spin system, the SU(2) J-Q model, by means of the unbiased worldline quantum Monte Carlo method. We found strong quantitative evidence for deconfined linearly dispersing spinons with multiple gapless points at k=(0,0), (π,0), (0,π), and (π,π). We also observed a duality between singlet and triplet excitations at the critical point and inside the ordered phases, in support of an enhanced symmetry, possibly SO(5).
References
Hidemaro Suwa, Arnab Sen, and Anders W. Sandvik, Phys. Rev. B 94, 144416 (2016).
Level spectroscopy in a two-dimensional quantum magnet: Linearly dispersing spinons at the deconfined quantum critical point

Fig. Low-lying energy spectrum at the deconfined quantum critical point. There are four gapless points for both S = 0 and S = 1 excitations, at k = (0,0),(π,0),(0,π), and (π,π). Close to these points the modes disperse linearly with the same
velocity. This figure is taken from Suwa et al., (2016).
Worm algorithm
The worm algorithm is a versatile technique in use of the Markov chain Monte Carlo method for both quantum and classical systems. In particular, the dynamic critical exponent of classical spin systems is significantly reduced, compared to the case of a single spin update. We improved the efficiency of the worm algorithm in combination with the directed-loop framework and the geometric probability optimization. In the case of the Ising model on the cubic lattice, our method is approximately 25 times as efficient as the classical worm algorithm and remarkably even more efficient than the Wolff cluster algorithm. Our approach can be applied to a wide range of physical systems, such as the |φ|^4 model, the Potts model, the O(n) loop model, the lattice QCD, and also some frustrated systems.
References
Hidemaro Suwa, Phys. Rev. E 103, 013308 (2021).
Geometric allocation approach to accelerating directed worm algorithm
Hidemaro Suwa, Phys. Rev. E 106, 055306 (2022).
Lifted directed-worm algorithm
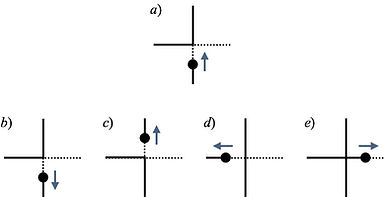
Fig. Example of worm moves on the square lattice. The solid (broken) lines show activated (deactivated) bonds. The solid circles indicate the kink (the head of the worm) breaking the loop constraint of activated bonds. This figure is taken from Suwa (2017).
Quantum Monte Carlo for spectral analysis
The worldline quantum Monte Carlo method is a powerful tool for quantum many-body problems, enabling estimates to be unbiased. Spectral information is, however, difficult to extract from Monte Carlo data. We formulated a convergent sequence for the energy-gap estimation in the worldline quantum Monte Carlo method. The ambiguity left in the conventional gap calculation is eliminated. The level spectroscopy from quantum Monte Carlo data is developed as an application of the unbiased gap estimation. From the spectrum analysis, we precisely determined the Kosterlitz-Thouless type quantum phase transition point in the spin-Peierls model. We demonstrated that the criticality at the transition point is described by the k=1 SU(2) Wess-Zumino-Witten model.
References
Hidemaro Suwa and Synge Todo, Phys. Rev. Lett. 115, 080601 (2015).
Generalized Moment Method for Gap Estimation and Quantum Monte Carlo Level Spectroscopy
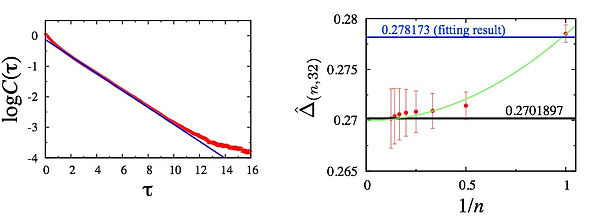
Fig. Example of the improved gap estimation for the antiferromagnetic Heisenberg chain of 16 sites. The left panel shows the imaginary-time spin-correlation function and the right panel shows our gap estimates. Our estimator is unbiased in the large n (and low temperature) limit, where n is the index of the estimators.
